PosrgreSQL 学习计划——索引之 B-Trees

数据库检索使用 B-Trees 和不使用索引的时间对比

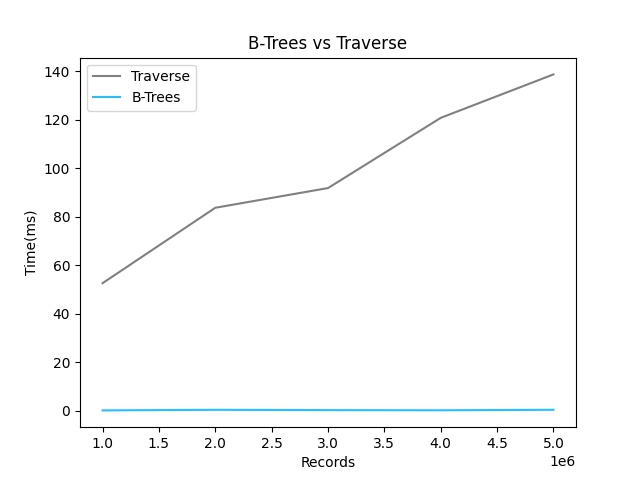
随着数据量的增长，遍历查询所用的时间也会线性增长，而使用索引后查询速度有极大的提升，本次学习会关注以下几点

什么是 B-Trees？
B-Trees 补充说明
B-Trees 查询、插入、删除示例

什么是 B-Trees？

英文好的同学移步：https://www.cs.utexas.edu/users/djimenez/utsa/cs3343/lecture16.html

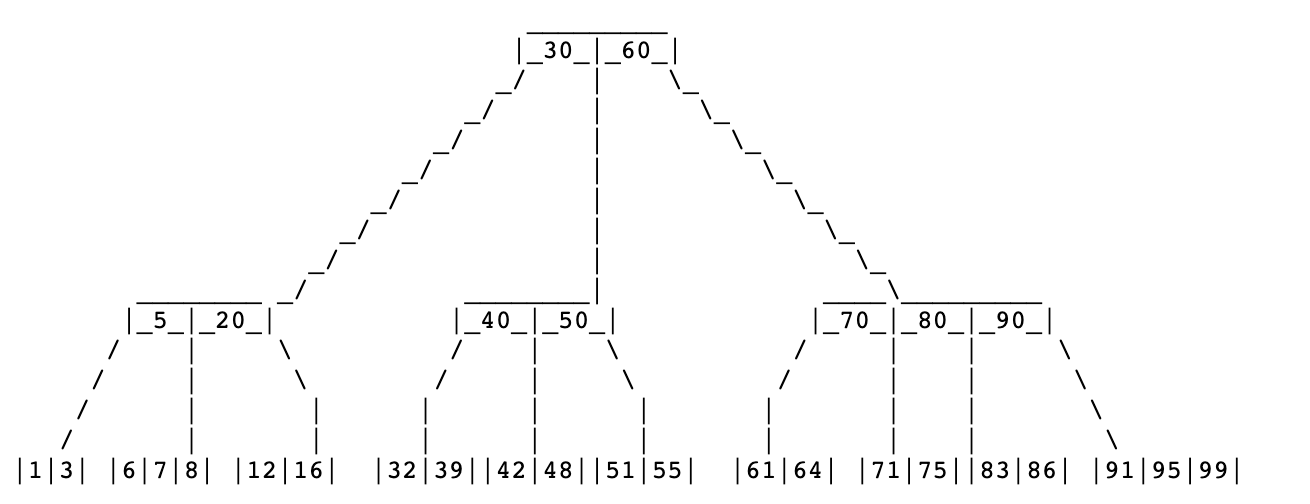
B-Trees 是二进制搜索树的变体，可以快速搜索磁盘上的文件。相较于二进制搜索树（Binary Search Tree，BST）的一个key，2个子节点，B-Trees 具有 n 个 key 和 n + 1个子节点，其中 n 可以很大。

这样就缩短了树的高度，与二进制搜索树相比，所需的磁盘访问量要少得多，相应的，B-Trees 算法更加复杂，比二叉搜索树需要更多的计算，但是这种额外的复杂性是值得的，因为计算比磁盘访问便宜得多。

重要的概念

There are lower and upper bounds on the number of keys a node can contain. These bounds can be expressed in terms of a fixed integer t >= 2 called the minimum degree of the B-tree:

Every node other than the root must have at least t-1 keys. Every internal node other than the root thus has at least t children. If the tree is nonempty, the root must have at least one key.

Every node can contain at most 2t-1 keys. Therefore, an internal node can have at most 2t children. We say that a node is full if it contains exactly 2t-1 keys.

节点可以包含的键（key）数有上限和下限，这些界限可以用固定的整数 t >= 2 表示，称为B树的最小度

除根节点外的每个节点都必须至少具有 t - 1 个关键字。因此，除根以外的每个内部节点都至少有 t 个子节点。如果树是非空的，则根必须至少具有一个键。
每个节点最多可以包含 2t - 1 个键。因此，一个内部节点最多可以有 2t 个子节点。我们说，如果节点恰好包含 2t - 1 个键，则该节点已满。

B-Trees 查询

示例：在树中搜索 120，首先从根节点开始比较。

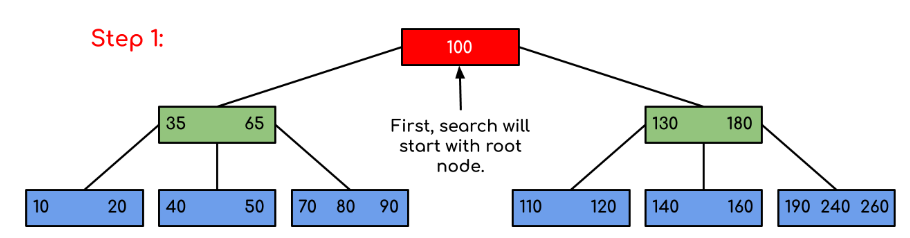
大于100，进入右子树，小于130，接着进入左子树

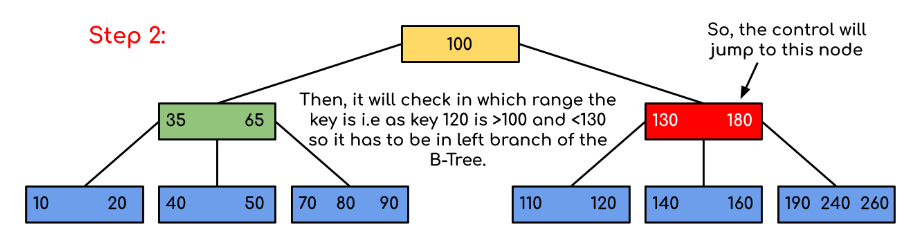
然后通过比较110，进而找到这个值

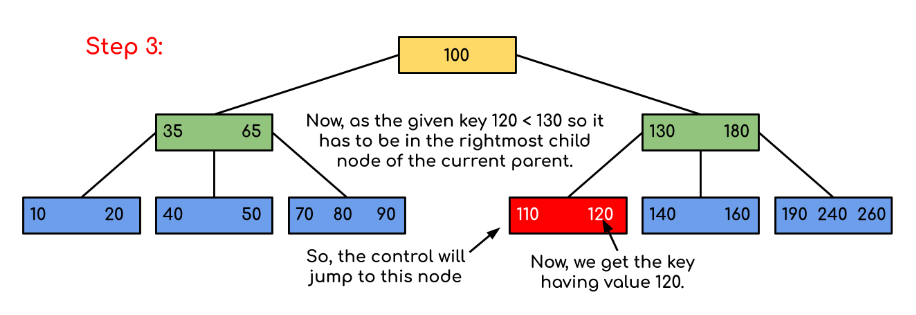
如果要搜索的数值是180，那么到Step2，就找到结束检索。

图片来自：https://www.geeksforgeeks.org/introduction-of-b-tree-2/ （原文有示例代码）

B-Trees 插入

示例：以 t = 3，插入 10, 20, 30, 40, 50, 60, 70, 80, 90 为例构建 B-Trees

最开始树为空，插入10，10 即为根结点。

然后依次插入 20，30，40，50，树的状态如下图，因为最多有 2t - 1个键，所以这个根结点容纳了 5 个键。

接下来插入 60，因为根结点已经满了，所以接下来会进行分割，60 将被插入到合适的位置。本例来看，因为 60 大于 30，又大于 50，所以 60 插入到了右子树节点键值右侧。

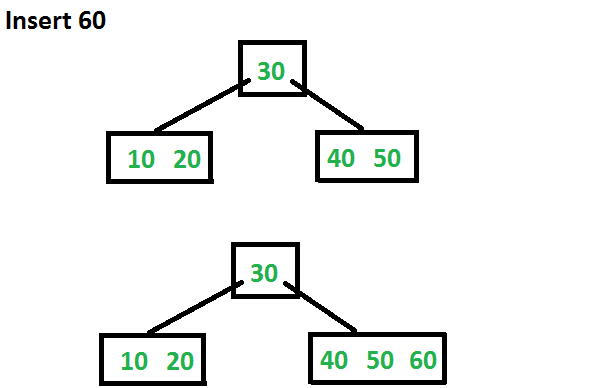
接下来插入 70，80 它们都被插入到了适当的位置，没有发生拆分。

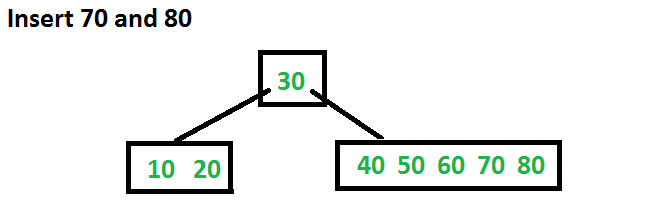
再次插入 90 会触发拆分，对比上图，右子树进行了拆分，60 被提升到根结点，重组后的树如下图。

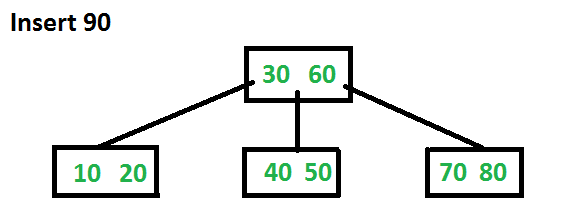
图片来自：https://www.geeksforgeeks.org/insert-operation-in-b-tree/（原文有示例代码）

B-Trees 删除

示例比较好理解，删除 F，M，G

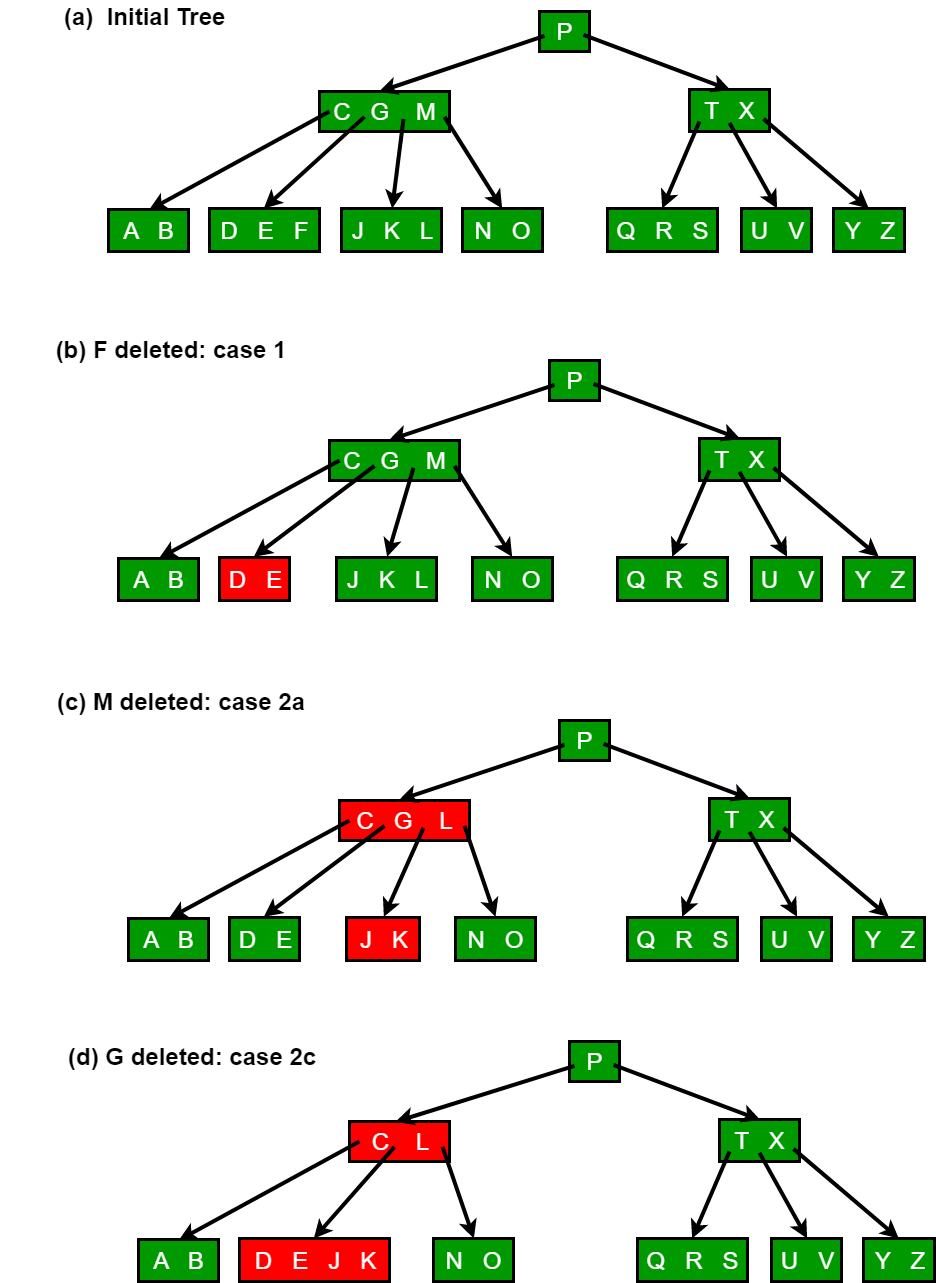
删除 D，B 结点

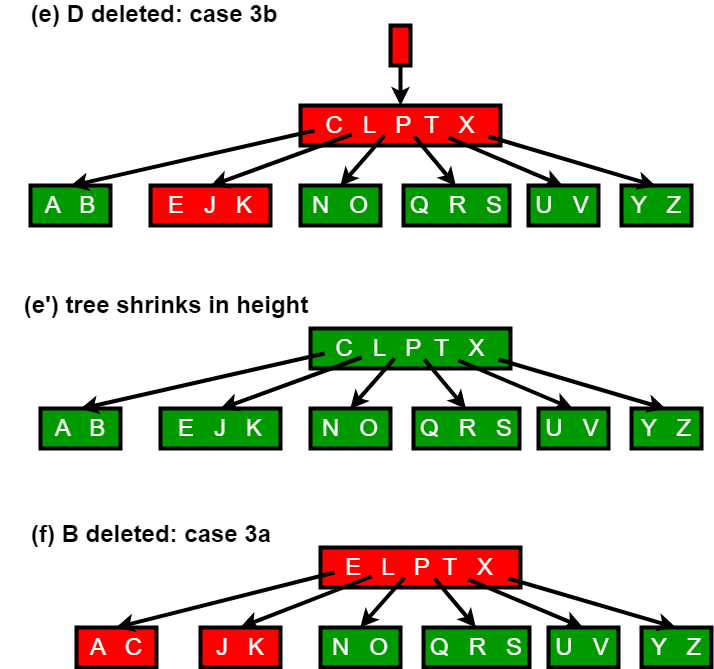
在 PostgreSQL 什么情况下应该使用 B-Trees 索引

如果不指定索引类型，PostgreSQL 默认使用的就是 B-Trees 索引。

B 树适合相等判断和有序的区间查询，通常来说，经常使用这些查询时推荐使用 B 树索引： <、>、<=、>= 以及 =。

此外，对于判断字符串开头的 LIKE 和 ~ 查询也可以考虑使用 B 树索引。比如： col LIKE 'foo%' 或者 col ~ '^foo'。

B 树对内容进行了排序，并不保证总是快于遍历查询，但大多数情况下都很有效率。

首图使用 Python 脚本自动生成，以下是建表语句与代码

t_numbers.sql

-- 创建 t_numbers 表
CREATE TABLE t_numbers(
  val integer,
  val_indexed integer
);
CREATE INDEX t_numbers_val_indexed ON t_numbers using btree (val_indexed);

代码：b-trees-and-traverse.py

-- 查询索引大小
SELECT pg_size_pretty(pg_relation_size('t_numbers_val_indexed')) AS size;

-- 查询表大小
SELECT pg_size_pretty(pg_relation_size('t_numbers')) AS size;

B-Trees 补充说明

B-Trees 是平衡树，即每个叶子节点到根节点的距离相同；
非二叉树，二叉树是每个节点有且只有两个叶子节点，平衡树则可以有多个叶子节点；
B-Trees 能够在 O(logN) 时间复杂度对叶子节点进行搜索、插入、删除；
关键字集合分布在整颗树中；
任何一个键出现且只出现在一个结点中；
搜索有可能在非叶子结点结束(树中所有结点都存储数据，与B+树这一点不同)；
其搜索性能等价于在关键字全集内做一次二分查找；

B 树的设计思想是将树拍扁，减少查询硬盘I/O的次数，从而提升性能。 B+ 树在 B 树的基础上进行了调整，在范围查询是拥有更好的性能，接下来学习 B+ 树。

参考