Chapter 1：内在有偏的样本

案例：“记者在火车上调查大家都买到了回家过节的车票”

第一章讲的是样本因自身特性或选择方式而无法代表总体，导致统计结果失真。

最基本的样本是随机样本，它是指完全遵循随机原则从总体中选出的样本。总体即形成样本的母体。 随机样本的检验方法是：总体中的每个名字或每个事物是否具有相同的几率被选进样本？ 纯随机样本是惟一有足够把握经受统计理论审查的样本。但它也有不足之处，在很多情况下，获得这种样本的难度很大并且十分昂贵，以至于单纯考虑成本就会排除它。

Chapter 2：精心挑选的平均数

案例：一个富豪年薪 1000 万，他有 9 个朋友穷光蛋，平均一看，各个年薪百万。

当你听到公司执行总裁或企业所有者宣称，在他的企业中员工的平均收人是多少时，你应该好好思考一下其中的原因。如果这个数是中位数，你可以获得一些显而易见的信息：一半员工赚得比它多，一半比它少。但如果是均值（请相信我，没有确切指出它的种类时，多半是均值），它仅仅是所有者 25000 英镑的高收入与全体工人低水平收入的平均数，根本没有什么意义。“平均年收入为 3800 英镑”既隐瞒了1400英镑的低收人，又隐瞒了所有者以巨额薪金形式抽取的高额利润。

所以，当你被告知某个数是平均数时，除非能说出它的具体种类——均值，中位数，还是众数，否则你对它的具体涵义仍知之甚少。

Chapter 3：没有披露的数据

案例：某人宣称抛硬币正反面的比例是 5：1，但是没有披露他做了 100 次试验，只选择了其中的 5 次试验结果作为样本进行统计

还有另一类没有透露的数据，它的遗漏也同样具有破坏性。这类数据表明了事物的变动范围以及与给定平均数的偏离水平。通常情况下，单凭一个平均数来描述事物过于简单，起不到作用，不管这个平均数是均值还是中位数，也不管平均数的具体类型是否已知。

Chapter 4：毫无意义的工作

案例：某公司投入巨额资金，部署了多条国际专线，调整了 BGP 路由策略，优化了跨境访问链路，最终成功地将国际网络访问速度从 300 毫秒降低了 2% —— 相当于 6 毫秒的提升。

只有当差别有意义时才能称之为差别

换句话说：

只有在毫无意义时，这个差别才如此值得强调

Chapter 5：令人惊奇的图形

案例：（见以下图像）

只需要改变横坐标与纵坐标的比例关系，将纵坐标的每一个刻度缩减为原来的1/10即可，没有人规定不能这么做，而这将会产生一张更加完美的图形。

显然图形比文字更有效，因为图形中不存在任何形容词和副词来破坏它所具有的客观性幻觉，而且谁也无法指责你。

搜索到某龙江省历年出生率数据（21 世纪），这是一个稀疏平常的折线统计图

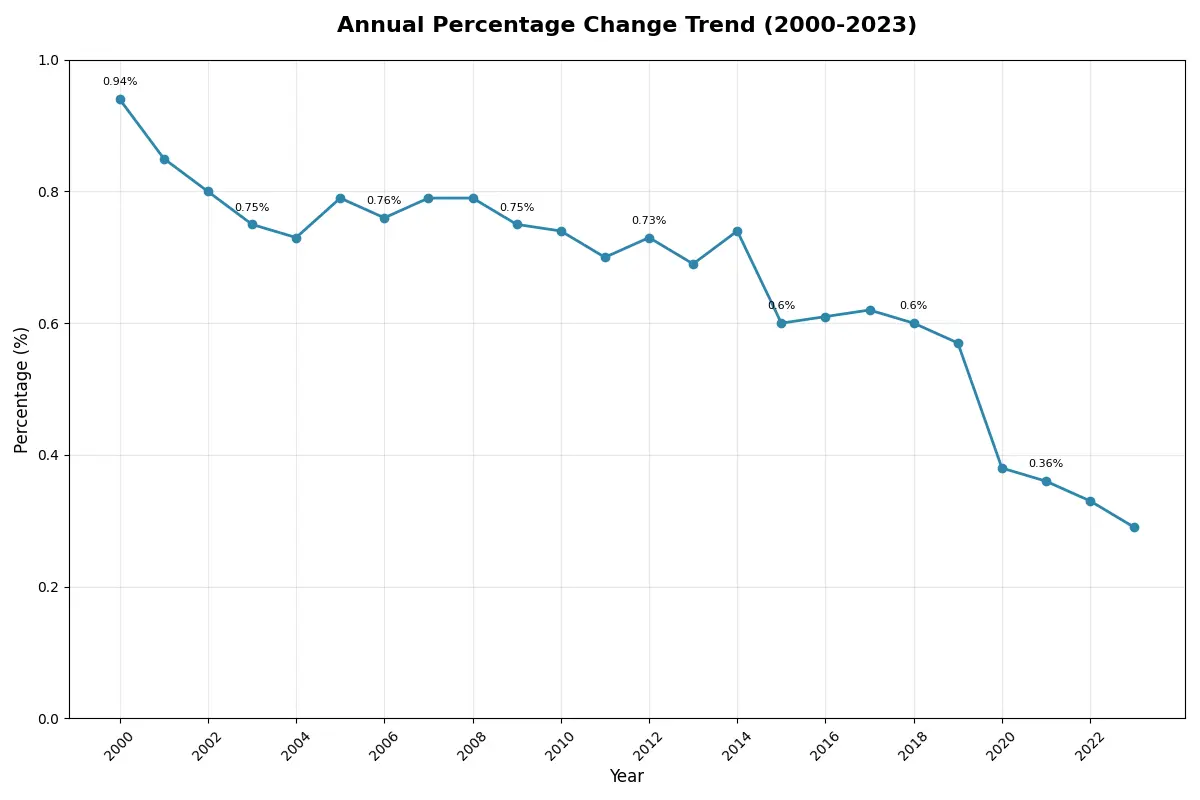
已经可以看到出生率下降比较多，如果我修改为下图的形式，宽高对调，同时 Y 轴间隔从 0.2 调整为 0.05，图像将更有震撼效果

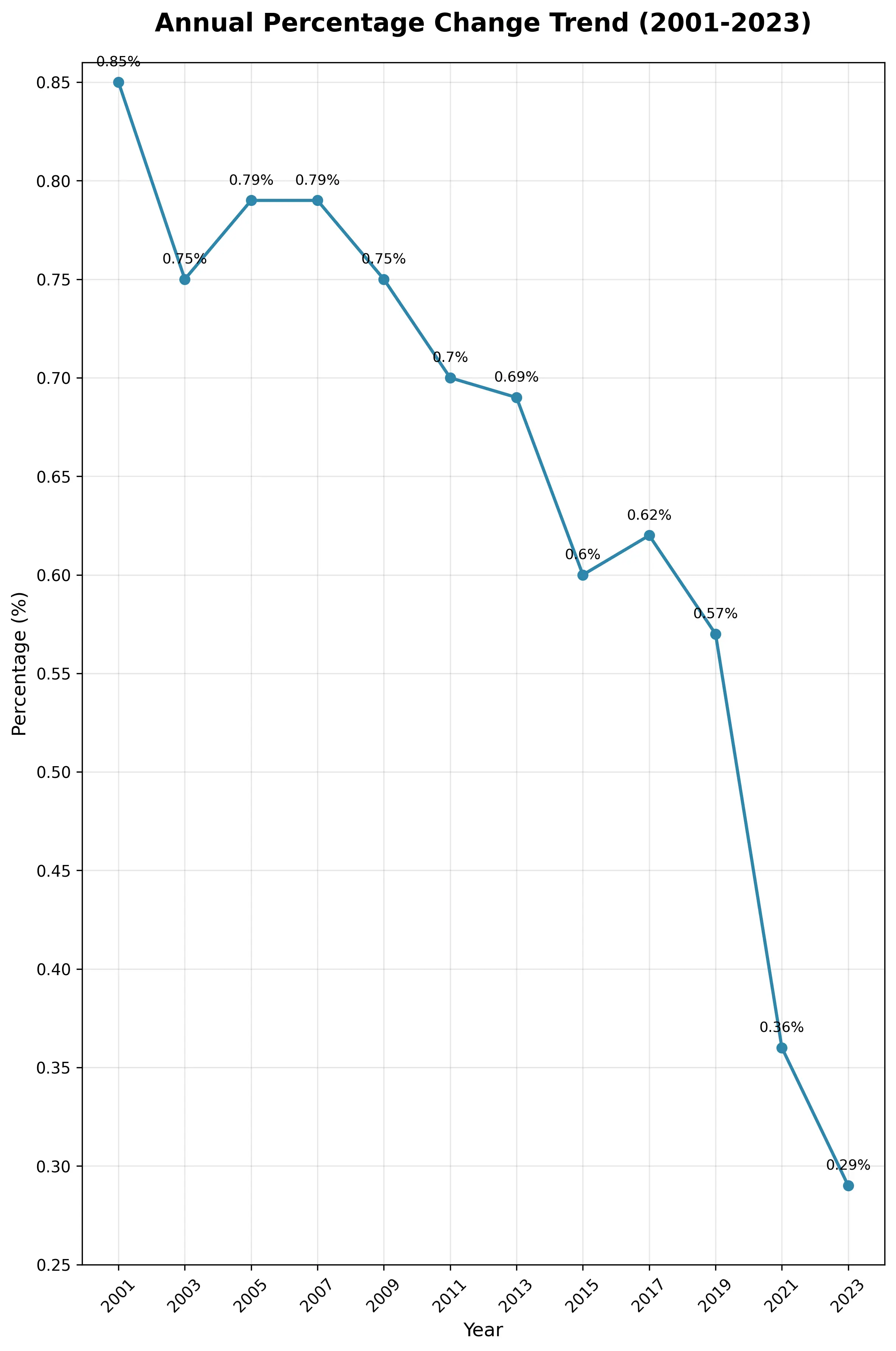
Chapter 6：一维图的滥用

案例：（见以下 AI 提供的说明）

在图表的世界里，只要敢缩轴、敢立体、敢堆图标，你就能让“微涨”看起来像“暴涨”

跟「令人惊奇的图形」类似，一维图像想要突出或降低一些视觉效果，可以做的文章很多

Chapter 7：不完全匹配的资料

案例：某诺贝尔奖得主每天都喝这种牛奶，但没有提及他也吃面包、鸡肉和沙拉，每天晨跑、骑自行车

如果你想要人相信 “结论A”，但拿不出证据，就展示一个听起来很像、但其实只是“相关”的 B。

这就是“不完全匹配的资料” —— 一种披着数据外衣的偷换概念

Chapter 8：相关关系的误解

案例：研究发现冰淇淋销量高的时候，溺水事件也多。

实际上是因为夏天到了，吃冰淇淋的人变多，游泳的人也变多，共同原因是 “气温升高”，不是冰淇淋和溺水互为因果。

重要的概念即：相关 ≠ 因果

“相关性”（correlation）只是两个变量一同变化，而“因果性”（causation）意味着一个是另一个的原因

但是，很多时候人们会误把 “同时发生” 当作 “有因果关系”——这是一个统计思维中的致命误区

Chapter 9：如何进行统计操控

案例：产品满意率达到 100%，其实只调查了 5 个人，这五个人还是公司的员工

任何建立在小样本容量上的百分数都可能产生误导，直接给出调查对象规模（样本容量）的大小将更有价值。

案例：股票跌了 10%，但是需要上涨百分之 11.11% 才能回到原来水平，下跌的越多，涨回去越难

50%的削减量需要通过提高100%才能加以补偿。

案例：商场打折，折上折的数字陷阱

份“50%折扣再打20%折扣”的报价单时，那并不意味着70%的折扣，实际上只有60%

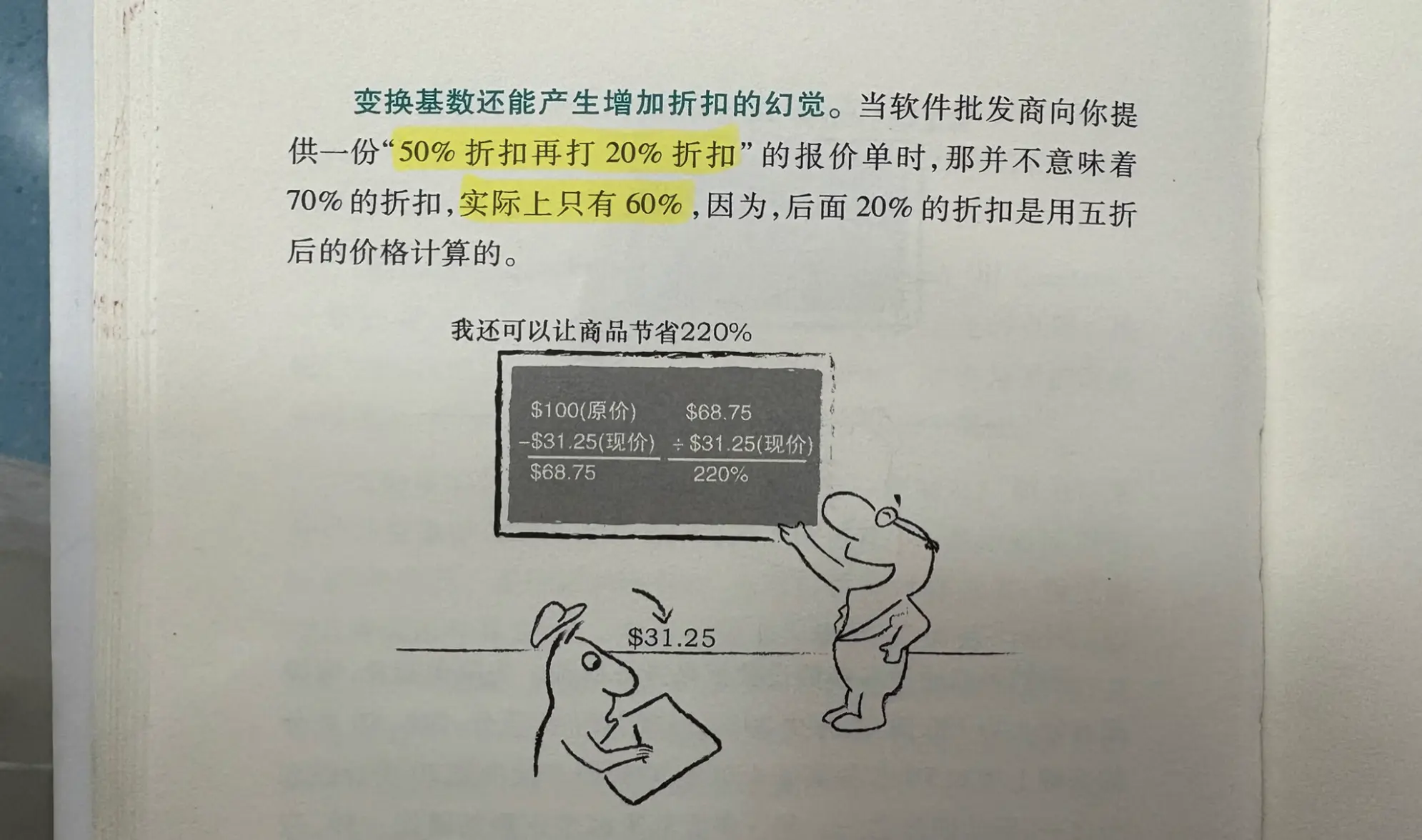
案例：（这个案例就很经典）

人们询问他的兔肉三明治为什么能卖到如此便宜的价格时，“哦，”他说，“我当然得掺一些马肉，但我的比例是一比一：一匹马，一只兔子。”

Chapter 10：如何反驳统计资料

省流：数字不是事实，只是说故事的工具，别轻信涨幅和图标，多问问数据怎么来的，多问问 AI 怎么看